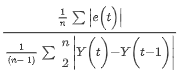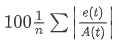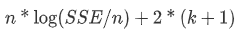预测描述

适用于： Tableau Desktop, Tableau Public

“描述预测”对话框描述了 Tableau 为您的可视化项计算的预测模型。

启用了预测后，您可通过选择“分析”> “预测”>“描述预测”打开此对话框。

“描述预测”对话框中的信息是只读的，不过，您可以单击“复制到剪贴板”，然后将屏幕内容粘贴到文档中。

“描述预测”对话框有两个选项卡：“摘要”选项卡和“模型”选项卡。

描述预测 —“摘要”选项卡

“摘要”选项卡描述 Tableau 已创建的预测模型，以及 Tableau 在您的数据中发现的一般模式。

用于创建预测的选项

此部分汇总了 Tableau 创建预测所用的选项。这些选项可由 Tableau 自动选取，也可在“预测选项”对话框中指定。

  • 时间系列 - 用于定义时间系列的连续日期字段。在某些情况下，此值可能实际上不是日期。请参见在视图中没有日期时进行预测。

  • 度量 — 估计值时使用的度量。

  • 向前预测 — 预测的长度和日期范围。

  • 预测依据 — 创建预测所用实际数据的日期范围。

  • 忽略最后的周期数 — 实际数据末尾的周期数将被忽略，该数值用于确定预测数据显示的周期数。此值由“预测选项”对话框中的“忽略最后的周期数”选项决定。

  • 季节模式 — Tableau 在数据中找到的季节周期的长度，如果在任何预测中都找不到季节周期，则为“无”。

预测摘要表

对于预测的每个度量将显示一个摘要表，用来描述预测。如果使用维度将视图划分为多个窗格，则会在每个表中插入一列，用来指示维度。预测摘要表中的字段包括：

  • 初始 — 第一个预测周期的值和预测间隔。

  • 相对于初始值的变化 — 第一个和最后一个预测估计点之间的差值。这两个点之间的间隔显示在列标题中。当值以百分比形式显示时，此字段会显示相对于第一个预测周期的百分比变化。

  • 季节影响 — 这些字段将针对具有季节性（随时间变化的重复模式）的模型而显示。它们将显示实际值和预测值的合并时间系列中上一个完整季节周期的季节组件的高值和低值。季节组件表示相对于趋势的偏差，因此会围绕零值变化，并且在整个季节内的和值为零。

  • 贡献 — 趋势和季节性对预测的贡献程度。这些值始终以百分比形式表示，且总和为 100%。

  • 质量 — 指示预测与实际数据的相符程度。可能的值为 GOOD、OK 和 POOR。自然预测的定义为：下一周期的值估计将与当前周期的值相同。质量以与自然预测相比较的结果表示，例如，“OK”表示相比自然预测，预测误差更小；“GOOD”表示预测误差要小一半以上；而“POOR”则表示预测的误差更大。

描述预测 —“模型”选项卡

“模型”选项卡提供了更详尽的统计信息以及预测下的霍尔特-温特斯指数平滑模型的平滑系数值。对于预测的每个度量将显示一个表，用来描述 Tableau 为该度量创建的预测模型。如果使用维度将视图划分为多个窗格，则会在每个表中插入一列，用来指示维度。表有以下部分：

模型

指定“级别”、“趋势”或“季节”组件是否是用于生成预测的模型的一部分。每个组件的值为以下值之一：

  • 无 - 模型中没有该组件。

  • 累加 - 该组件存在，并且已添加到其他组件中以便创建整体预测值。

  • 累乘 - 该组件存在，并且已与其他组件相乘以便创建整体预测值。

质量指标

这组值提供有关模型质量的统计信息。

值定义
RMSE：均方误差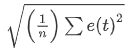
MAE：平均绝对误差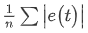

MASE：平均绝对标度误差。

MASE 测量误差量级与向前一期天真预测的误差量级的比率。天真预测法假定不管今天是什么值，明天都将是相同的值。因此，MASE 为 0.5 意味着您的预测的误差可能是天真预测误差的一半，这要优于 MASE 1.0，MASE 1.0 意味着您的预测并不比天真预测准确。由于这是为所有值定义的规范化统计数字并平均地衡量误差，因此是比较不同预测方法的质量的理想指标。

与更常用的 MAPE 指标相比，MASE 的优点在于：MASE 是为包含零的时间系列定义的，MAPE 则不是。此外，MASE 为误差赋予相等的权重，而 MAPE 为正误差和/或极值误差赋予更多权重。

MAPE：平均绝对百分比误差。

MAPE 测量误差量级与数据量级的百分比。因此，20% 的 MAPE 要优于 60% 的 MAPE。误差是模型估计的响应值与数据中每个说明性值的实际响应值之间的差异。由于这是一种规范化统计数据，因此可用于比较 Tableau 中计算的不同模型的质量。但是，对于某些比较，它可能不可靠，因为它对某些种类的误差设置的权重要大于其他误差。此外，对于包含零值的数据，其效果也不明确。

AIC：Akaike 信息准则。

AIC 是一个模型质量度量，由 Hirotugu Akaike 开发，可对复杂模型进行罚分以防止过度拟合。在该定义中，k 是估计参数的数量，包括初始状态，SSE 是误差平方和。

在上面的定义，用到的变量如下：

变量含义
t时间系列中的周期的索引。
n时间系列长度。
m一个季节/循环中的周期数。
A(t)周期为 t 时的时间系列的实际值。
F(t)周期为 t 时的拟合值或预测值。

残数为：e(t) = F(t)-A(t)

平滑系数

根据数据的级别、趋势或季节组件的演变速率对平滑系数进行优化，使得较新数据值的权重大于较早数据值，这样就会将样本内向前一步预测误差最小化。Alpha 是级别平滑系数，Beta 是趋势平滑系数，Gamma 是季节平滑系数。平滑系数越接近 1.00，执行的平滑越少，从而可实现快速组件变化且对最新数据具有较大依赖性。平滑系数越接近 0.00，执行的平滑越多，从而可实现逐渐组件变化且对最新数据具有较小依赖性。

 

回到顶部
感谢您的反馈!您的反馈已成功提交。谢谢!